核心算法介绍
核心算法
核心算法:基于梯度的非线性学习强度调节算法
Gradient-driven Nonlinear Learning Intensity Regulation(NLIRG)
算法简介
NLIRG(基于梯度的非线性学习强度调节算法)是一种智能训练优化技术。简单来说,它就像一位经验丰富的教练,能够:
- 智能识别难度:实时判断每个训练样本对模型来说有多难
- 动态调整强度:根据难度自动调整训练强度
- 防止过拟合:避免模型过度记忆训练数据而失去泛化能力
通过使用NLIRG,可以让模型在训练过程中,实时监测训练样本的难易度,并根据样本的难易度,动态调整训练强度,从而实现模型训练的调优,同时又缓解了模型的过拟合。
具体的说,我们为模型训练定制了一条曲线,使用损失来衡量模型训练的难度,并根据损失曲线,动态调整训练强度。
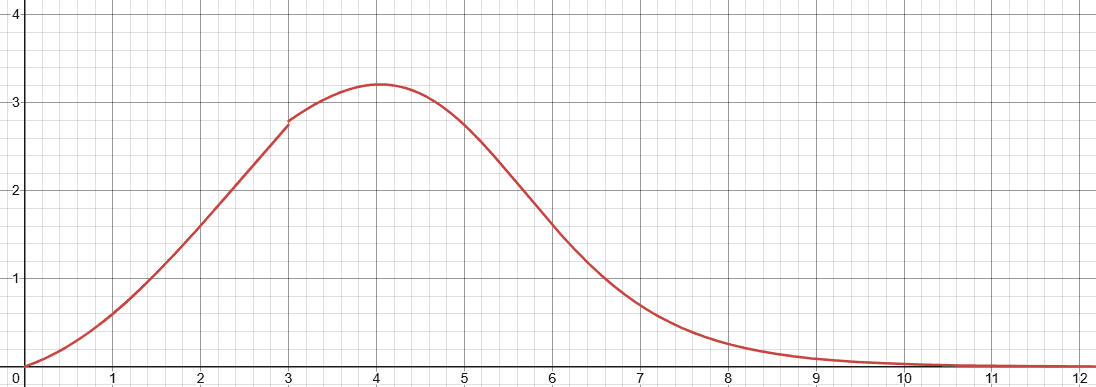
横坐标代表Loss值,纵坐标代表梯度计算权重。
核心算法函数
def dynamic_sigmoid_batch(losses, max_lr=1.0, x0=1.2, min_lr=5e-8,
k=1.7, loss_threshold=3.0, loss_deadline=15.0):
"""
NLIRG核心算法:基于损失值的动态权重计算
参数说明:
- losses: 损失值张量
- max_lr: 最大学习率权重 (默认: 1.0)
- x0: 第一个sigmoid函数的中心点 (默认: 1.2)
- min_lr: 最小学习率权重 (默认: 5e-8)
- k: sigmoid函数的斜率 (默认: 1.7)
- loss_threshold: 损失阈值,区分不同区间 (默认: 3.0)
- loss_deadline: 损失上限,超过此值梯度归零 (默认: 15.0)
返回:权重张量,用于调整反向传播的梯度
"""算法原理
NLIRG算法是一种基于现有模型训练的梯度下降算法改进。我们认为,模型训练的难易度与损失值的分布密切相关,因此,我们将损失值分布曲线作为模型训练难易度的衡量标准。
着重训练对模型有较大影响的Token,可以有效缓解模型过拟合。为防任务对模型过难,我们将损失值分布曲线分为四个区间,并根据区间对应的损失值,动态调整训练强度。
此算法详细计算每一token的损失值,并根据损失值计算对应token的权重值,将损失与权重相乘得到一个最终损失值用于反向传播。
权重计算策略:
| 损失区间 | 策略 | 目的 | 实际效果 |
|---|---|---|---|
| 低损失区间 (loss ≤ 1.45) | 削减梯度 | 避免过拟合 | 防止模型过度记忆简单样本 |
| 中等损失区间 (1.45 < loss < 6.6) | 增强梯度 | 快速学习 | 重点训练对模型有挑战性的样本 |
| 中高损失区间 (6.6 < loss < 15) | 削减梯度 | 避免过拟合 | 防止模型被困难样本带偏 |
| 高损失区间 (loss ≥ 15.0) | 梯度归零 | 避免异常样本影响 | 忽略明显错误的训练样本 |
以下是动态权重的计算公式:
其中 是损失值。
训练技巧:分批次的Token训练
此算法对Token损失的精确性要求较高,为保证Token的损失计算准确性,我们将Token分批次进行训练,一次只训练少量Token,保证Token的损失计算大致准确。
为什么需要分批次训练?
- 精度保证:小批次训练能更精确地计算每个token的损失
- 内存优化:避免一次性处理过多token导致显存溢出
- 梯度稳定:小批次训练有助于梯度计算的稳定性
实际应用:在SFT训练中,通过--token_batch参数控制每次反向传播的token数量
训练顺序调整算法
使用此工具可根据语料训练的难易度调整指令微调语料的顺序。
算法原理
我们认为,模型训练的难易度与损失值、熵的走向相似度密切相关,因此,我们将损失值、熵的相似度作为模型训练难易度的衡量标准。
核心思想:通过分析模型对每条语料的响应模式(损失值和熵的变化),评估语料的相对难度,难易结合,合理设置学习顺序。
数学表达: 设对特定一条语料的损失值矩阵为,熵向量为,则此语料的相似度为:
通过对语料的相似度进行排序,即可调整语料的训练顺序。
实际应用:
- 再训练之前排查语料问题,检查得分较低的语料是否编写错误。
- 平衡语料难易顺序,逐步训练。注意:简单的将语料从易到难进行训练,实际测试效果并不如混合进行。
How is this guide?